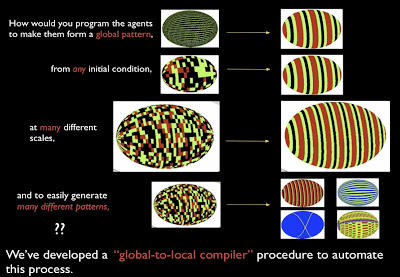
One major difficulty in self-organizing multi-agent systems research is the lack of theoretical models that allow us to ask fundamental questions about computability and complexity. Given a global goal and a multi-agent system where the agents have limited capability (finite state, limited view), we can ask many theoretical questions: Is the global task solvable? What are the minimal agent capabilities required to robustly solve the task? What are the lower bounds on parallelism and scalability? Answers to these theoretical questions have important practical implications: they tell us fundamental limits on what global-to-local algorithms and compilers can achieve, and how agent design restricts the set of tasks that the system is able to solve.
We have developed the beginnings of a global-to-local theory that can answer such questions, in the context of self-organizing pattern formation tasks on 1D asynchronous cellular automata. This work was developed by Daniel Yamins (now faculty at Stanford) during his PhD. It is inspired in part by the amazingly robust and complex pattern formation that is achieved by biological systems such as the fruit fly embryo, as well as the engineering application of pattern formation ideas to robot swarms, modular robots and self-assembly.
Some of the contributions of this work are:
-
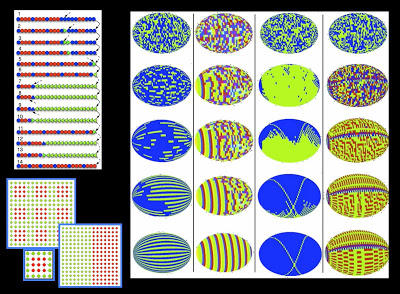
Yamins showed that there is a necessary and sufficient condition, Local Checkability, that not only allows us to answer the question of existence, but also produce minimal state agent programs for self-repairing pattern formation. Local checkability can be thought of as a distributed voting (or stopping) condition and can be used to solve three problems.
- An existence problem: Local checkability forms a simple criterion that any robustly solvable goal must satisfy. If a pattern is not locally checkable, no robust local rule can self-organize it. The minimum radius for local checkability gives us a way to reason about minimal agent programs. We have used local checkability to show lower bounds on agent state and communication for several common classes of patterns (repeated, scale-invariant).
- A construction problem: For all patterns that are locally checkable, we can use the local check to algorithmically derive local rule that generates it robustly. The local agent rule is by construction scale-invariant (works for varying numbers of agents), robust (works for any initial condition and asynchronous timing), and self- repairing (pattern reemerges after perturbation).
- A resource problem: The two main resource parameters of the model, the agent interaction radius and agent memory size, exist in a radius-state resource tradeoff. We describe algorithms for tuning along the continuum between large-radius/low-state and low-radius /high-state implementations.
- By combining these three techniques, we are able to build a Global-to-Local Compiler that implements this theory: the compiler takes as an input a logic-based description of a pattern or a set of example patterns, derives a local checkability condition, and produces a cellular automata rule that is both scalable and self-repairing.
This work has led to many new insights into current global-to-local compilers, for example how efficient they are in terms of agent state and time. It has also revealed new and surprising connections between cellular automata and traditional computing models (such as Turing machines, Languages, and De-Bruin graphs). An important future area will be generalizing this work from cellular automata to other multi-agent settings, and using this model to better understand existing self-organizing systems. Ultimately, this type of theory will provide an important design tool for self-organizing systems, by allowing us to reason about the complexity and scalability of embedded multi-agent systems where agents have limited capability.